Liquidity pools: Everything you need to know

Liquidity pools: Everything you need to know

How much token liquidity is needed in a liquidity pool? What are the considerations you need to take into account a when setting up a liquidity pool? How do liquidity pools work anyway??

Liquidity pools are a key part of web3 projects and I’ll be answering all of these questions in this article.

Token liquidity, the ability to buy and sell tokens, is a core part of tokenomics and any web3 project. Liquidity pools, the key innovation that enables this, are one of the most elegant, important, and yes, coolest, parts of DeFi. Liquidity pools are the basis for two key parts of DeFi:

1. Free trading tokens between anything and everything — without anyone’s permission and without passing through any gatekeeper (which forms the basis of the DeFi Matrix).
2. The basis of yield and the opportunity cost of capital in DeFi.

All in all, having a good understanding of liquidity pools, how they work as a user, investor and builder, are important parts of understanding and designing tokenomics.

In this article I’ll cover:

1. What are liquidity pools
2. How liquidity pools work
3. The implications that price slippage, arbitrage and Impermanent Loss in liquidity pools have on investors, builders and users.

In a follow up article I’ll walk you through how to setup a liquidity pool for your own project and the things to consider.

What are liquidity pools

Liquidity pools are a mechanism that allow trading between two tokens in a completely decentralized way. This is as opposed to the traditional method which is managed by a centralized market maker who matches orders to buy and sell in an order book (think going to the bank to exchange dollars for euros). Liquidity pools use smart contracts instead of the centralized market maker. They determine the asset prices with an algorithm that takes into account the ratio between the two tokens in the liquidity pool. Because this all happens automatically, they are called ‘Automated Market Makers’, or in short: AMMs.

Imagine a bowl where you put in two different currencies: dollars and euros. The bowl is left out in the open so that anyone can trade dollars for euros, whenever they want. Trading costs a small fee, which goes to reward the people who provided the liquidity. Anyone can add dollars and euros (i,e liquidity) to the bowl and receive their fair share of the reward fee. Because all of this runs on open source code, anyone can create a pool between any two assets.

How liquidity pools work

Their are three main components to a liquidity pool:

1. Providing liquidity: what tokens will trade with each other
2. Setting the price of the tokens: the pricing algorithm
3. Rewarding liquidity providers (LPs)

Liquidity pools: providing liquidity

Liquidity pools can be set up by anyone using protocols such as Uniswap or Sushiswap (on Ethereum). Every blockchain has its most popular AMM protocol as well as some competitors. Pools are established by depositing two different tokens into the pool. The tokens can then be swapped with each other. For example depositing ETH and USDC into a new liquidity pool will create a pool where one can trade ETH with USDC.

How liquidity pools are structured. Source: Uniswap

Once a pool has liquidity, anyone can swap between those two tokens. The question now becomes: at what price?

Liquidity pool price setting

Price between assets is set by using a formula that reflects the ratio between the two assets. When the pool has more A tokens than B tokens, it costs more A tokens to buy one B token. For example if a pool has 10 ETH and 1000 USDC, the ratio between ETH:USDC is 1:100, essentially giving ETH a current price of 100 USDC per ETH.

The formula that gives the exact price is quite simple (which is part of what makes liquidity pools so elegant) and is called the “constant product” formula: X * Y = K.

The constant product formula looks at the pool assets before a swap happens: how many A tokens and B tokens are in the pool. It then creates ‘K’, the constant, by multiplying the number of A tokens by the number of B tokens. Using the constant, it’s now possible to calculate the price of token A in token B terms.

For example a pool has 10 ETH tokens and 1000 USDC tokens. The ‘K’ value will be 10,000 (because 10 * 1000 = 10,000). Now, to calculate the price of ETH, all we have to do is solve a simple equation with no missing variables, giving us the price of 100 USDC per ETH. The math is actually quite simple. If you’d like to review it (recommended) this is a great 7:30 minute video to watch.

While it’s good to understand the math, in tokenomics terms, what mainly matters is understanding the implications the ‘constant product formula’ has on token prices in, and outside the pool. These implications matter to you whether you’re setting up a liquidity pool or trading.

The main implications are:

1. Assets traded in a pool have price slippage. You have to be aware of the ratio between the volume of any given trade and the Total Volume Locked (TVL) inside the pool.
2. Pool prices can deviate significantly from prices on other exchanges. For example the ETH/USDC price in the pool can be very different from trading ETH/USDC on Coinbase or another exchange.
3. Liquidity providers can suffer from ‘Impermanent Loss’ and need to be compensated for that.

Let’s break down each of these implications more in depth.

Price slippage in liquidity pools

The x * y = k formula results in a very specific way that trading one asset in the pool for another works. It’s a curved function that looks like this:

Any point on the curve is denominated in an amount of A and B tokens in the pool. The ratio between them sets the price. A pool with 100 A tokens and 2 B token means that 50 A tokens are needed to get 1 B token¹.

When token ratios become extreme and move towards the edges of the curve, the cost to swap between the abundant token and the depleted token rises exponentially making it more and more expensive.

Every successive trade moves the token price significantly. This movement is called price slippage. While it occurs in every AMM trade, it is more impactful the more extreme the ratios become.

As you can see in the curve dynamic, as the pools reach their extremes, the curve flattens out towards infinity — meaning that a curve can never be fully depleted! Since the less A tokens we have in the pool, the more B tokens we’ll need to pay for it, when the pool reaches near the end of its A tokens, the price will sky rocket towards infinity B tokens per A token.

Price slippage has significant effects on the price of tokens and needs to be managed carefully else it can be taken advantage of by traders. The main way to reduce slippage is by having lots of liquidity in a pool in relation to each trade. The lower volume the trade is in relation to the amount of liquidity in the pool, the less price will fluctuate.

For example a trade that looks to swap 10% of the TVL amount in a pool will move the price roughly 9% while a trade that swaps 0.1% of the TVL will move the price only 0.09% — barely budging it.

Simply: More liquidity means a larger range of trading with low slippage and a more stable price.

Price arbitrage

The second implication to be aware of is that the price of the tokens in a liquidity pool can be significantly different from the prices of those tokens on other exchanges!

Because the price in a pool is set purely by the constant product formula, no external variables affect the pool token prices. The only things that affect the prices are actual trades: the amount of liquidity in the pool and the volume, or size of the swap, that someone wants to trade.

For example, in a low volume ETH/USDC pool one trader could move the price of ETH in USDC terms to an extreme. But that wouldn’t affect the price of ETH on any other exchange such as Coinbase, Binance or any other AMM either!

This opens the door for market and price manipulation as well as arbitrage opportunities. If the price of tokens in a liquidity pool are materially different from those on external exchanges, an arbitrageur should enter the market and arbitrage the opportunity away, bringing the prices across AMMs and other exchanges into equilibrium.

What this means for builders is that if you’re using your AMM as the oracle price feed for any applications, governance or DeFi — you need to be aware that it’s not a question of is it possible, rather it’s only a question of how much money it will cost someone to manipulate your prices to the extreme. As a user or investor, you’re best always checking other exchanges to see if you’re getting a market price.

Impermanent Loss

Impermanent loss (IL) is the possible loss of value that an LP can suffer by committing assets to a pool compared to simply holding the same assets. As in a LP holding ETH and USDC could see more price appreciation in some cases than by adding ETH and USDC to a liquidity pool.

How does this happen? It’s relatively simple to calculate, but intuitively, when you put 1 ETH and 100 USDC into a liquidity pool, in a way you’re giving up a little bit of the upside if the price of ETH goes up. Why? Remember that the assets in a liquidity pool are always balanced in value. This means that the pool automatically ‘gives away’ a portion of the price appreciation to make sure the constant product formula stays true.

Here’s an example:

1. The price of ETH goes up in the market (outside of the liquidity pool) from 100 to 120 USDC per ETH.
2. Arbitrageurs see an opportunity to buy ETH in the liquidity pool for 100 USDC and sell it on the market for 120 USDC (a nice 20$ profit). This brings the price in the pool to an equilibrium with the rest of the market.
3. Using the constant product formula the balance of tokens in the pool is now 0.91 ETH and 109 USDC (giving a price of ~120 USDC per ETH).
4. Your LP stake is now worth in dollar terms: (0.91 * 120) + 109 = 218.2. If you had simply held your 1 ETH and 100 USDC in a wallet, it would be worth 220. You’ve suffered impermanent loss of 1.8!

This happens because of the inherent rebalancing that occurs in constant product formula AMMs. It’s called Impermanent Loss because if the price of ETH dropped from 120 USDC to 100 USDC, the loss would disappear. The loss is dependent on price fluctuations. The large the price movement in the base assets, the larger the IL.

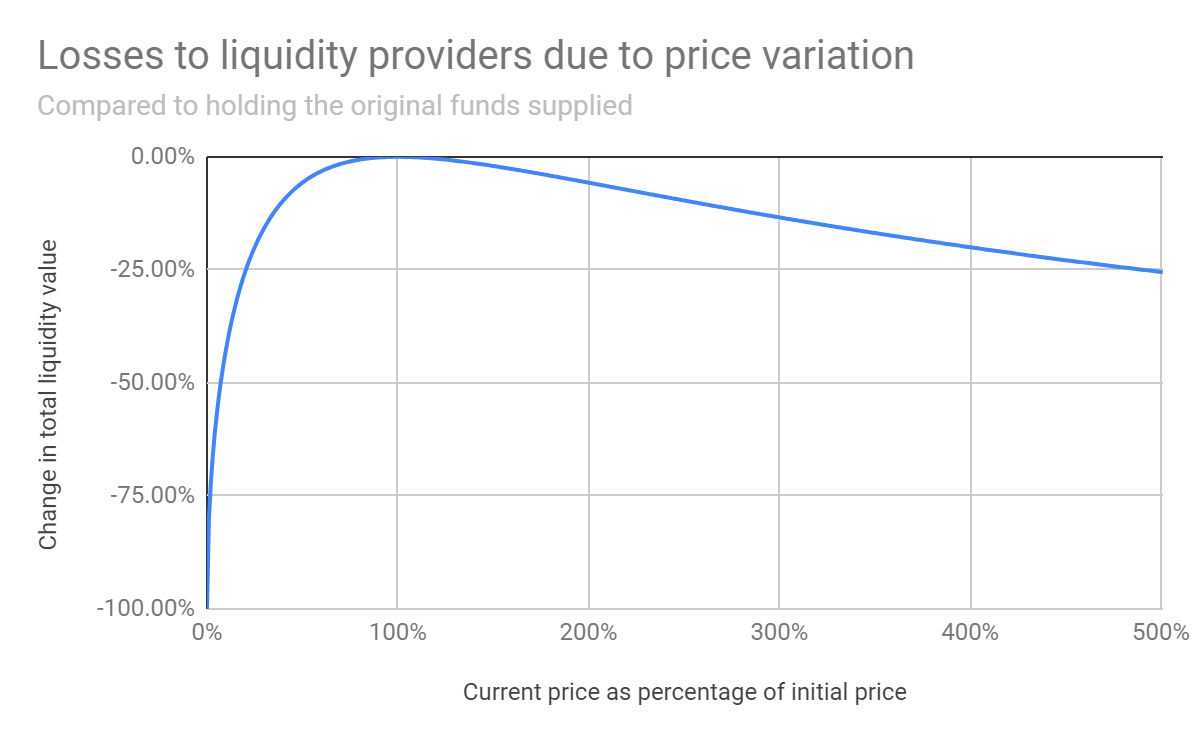
It’s important to note that the loss isn’t in absolute terms, only relative to holding the assets outside of the liquidity pool. The important implication for an LP in this case is that the risk of IL increases an LPs risk when adding liquidity.

LPs have two financial risks that need to be mitigated: opportunity cost and IL. This is what the AMM trading fee goes to mitigate. The higher the risk, the higher the fee that LPs can expect to receive. Higher risk can generally be quantified into two buckets: how long capital we need to be used as liquidity and the volatility of the underlying assets. The longer the lock up and the more volatile the underlying assets, the more fees an LP can expect to receive.

Since most projects use the Uniswap protocol (or something similar) most have a straightforward fee of 0.3% per trade — usually not nearly enough to compensate LPs for their risk. This is why most projects reward LPs with additional tokens. Without these additional tokens, the benefits of providing liquidity for a project don’t outweigh the risks and since projects know that liquidity is critical for their token, they need to allocate their budget accordingly (more on this topic here).

Liquidity Pools: the core DeFi building block

DeFi is built on constant product AMM liquidity pools. It’s these trust-less, permission-less liquidity pools that form the DeFi Matrix and the basis of yield in DeFi.

Understanding the core concepts of how prices are set, how prices can change or be manipulated and the implications for builders, users and investors is an important part to designing tokenomics.

Footnotes:

1. This is an over simplification to get the point across. An actual swap trade needs to add tokens to the pool thereby changing that ratio based on the constant K. AMM fees also need to be taken into account.